This post is part of a series on differential privacy. Check out the table of contents to see the other articles!

---

What is a good value of \(\varepsilon\) for differential privacy deployments? In a previous post, I visualized the privacy impact of different choices using this graph.

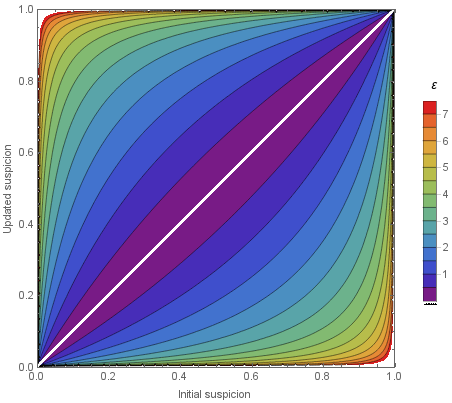
It quantifies the attacker's knowledge gain about an individual, depending on \(\varepsilon\). According to this visualization, \(\varepsilon\) values above 5 don't look great. Let's say we're using \(\varepsilon=7\). Suppose our attacker starts off with a small suspicion about their target (say, a prior of 10%). After seeing the output data, they get almost perfect certainty, with a posterior of more than 99%! Not a great privacy guarantee.

Yet, in real-world deployments, large \(\varepsilon\) values seem to be fairly common! This is pretty surprising. We use DP because it's supposed to give us a strong privacy guarantee. But this story seems to break down with such large parameters…

So, why are practitioners choosing such large \(\varepsilon\) values? Are these guarantees meaningless? How worried should we be? If you want to deploy differential privacy for a real-world use case, should you be willing to make the same choice?

First, the bad news: right now, we simply don't have a simple, clear-cut answer to these questions. Ask 10 differential privacy experts, and you'll likely get 10 different answers.

What I'll do in this post is less ambitious: I'll try to shed light on possible ways to look at the problem, using a fictional use case. Then, I'll give you real-world examples of deployments who used some of these ideas. This won't settle the debate, but hopefully this can help you grapple with these questions.

So. Suppose that we have a dataset about people's visits to different hospitals. We want to use it to train a machine learning model to predict the duration of future hospital stays. This model will be made public, so we want to use DP to protect the original data. But in the prototyping phase, we encounter a difficulty: we discover that we need a very large privacy budget — say, \(\varepsilon=42\)¹ — to get acceptable utility. We tried different ways of doing the training, and this is the best we can get.

What should we do?

Step 1: Improve the privacy accounting

A first question we should ask ourselves is: is this guarantee the best we can get for our algorithm?

How did we train our model in a DP way? Most likely, we ran different DP building blocks to do complex operations on our data. Then, we used the composition property to combine the budgets used at each step. This gave us our \(\varepsilon\) above: the total privacy guarantee of our process.

This process is called privacy accounting, and it can often be optimized. We could use DP variants or other smart ways to quantify the privacy loss. We might be able to take into account the structure of the data to make better use of parallel composition. Or use amplification results. Or even composition theorems that are specific to certain mechanisms. All these tools might give us a better privacy guarantee for our program… without changing the program itself!

Privacy accounting only ever gives us an upper bound on the actual privacy risk. We know for sure that risk is lower than this bound. But it might be possible to do the math in a different way and show something stronger. This won't help in very simple cases, for example if we're releasing a single histogram: there, we know the best possible way to measure the privacy loss, so the bound will be tight. But sometimes, we want to use much more complex algorithms, like ML training or synthetic data. For those, existing composition theorems might not be optimal. As a result, the advertised privacy guarantee is likely a pessimistic estimate. Maybe theorems and DP tooling will improve… and later, we'll realize that our guarantee was better than what we thought at first.

In our example, maybe we can get from \(\varepsilon=42\) to \(\varepsilon=21\) by optimizing the privacy accounting. Still pretty large, but better than before. What should we do next?

Step 2: Analyze the privacy guarantees more finely

The value of \(\varepsilon\) only tells a partial story about the privacy guarantee of a deployment. Another critical piece of information is the privacy unit: what are we actually protecting? Our \(\varepsilon=21\) guarantee from earlier applies to individual people. We'll protect someone's data even if they made many visits to different hospitals.

Can we complement this guarantee, and quantify the privacy loss of smaller pieces of data? For example, does our process provide a better guarantee to individual hospital visits? What about the information about a single diagnosis that a patient received? Also, does the privacy guarantee apply to everyone uniformly? Or is the \(\varepsilon\) upper bound only reached for a few outlier patients?

Let's try to answer these questions for our example. By doing some more analysis, we could discover the following additional guarantees.

• Each individual diagnostic is protected with \(\varepsilon=2\).
• Each individual hospital visit is protected with \(\varepsilon=7\).
• 75% of the people in the dataset only have a single hospital visit (so their \(\varepsilon\) is 7) while 15% appear in two (so their \(\varepsilon\) is 14).

This does not change our overall worst-case bound. But it gives us a more complete understanding of the privacy behavior of our program. It might make us more comfortable about deploying it.

Still, some of these numbers are pretty high. What now?

Step 3: Run some attacks

Privacy accounting gives us a guarantee against a worst-case attacker: someone perfect background knowledge and infinite computational power. And this attacker targets the most vulnerable data point in our dataset. So our high \(\varepsilon\) might not always reflect a realistic attack scenario. It makes sense to wonder: what about more realistic attackers?

To answer this question, we need to perform an empirical analysis of privacy risk: run an attack on our system in a realistic setting, and quantify the success of this attack. This isn't easy: a lot of evaluations are deeply flawed, and automated metrics are often meaningless. We will likely need to get expert help to run the attack. But this can still be worth doing! Attacks will often reveal interesting findings about the algorithm or its implementation.

If we do our best to run attacks, and they don't seem to perform well… this can raise our confidence in the privacy behavior of our mechanism. This won't give us a robust, future-proof guarantee like DP: someone could come up with a better attack in the future. But this can still give us a more nuanced picture of the practical risk. And, again, make us a little more comfortable about our deployment.

What if that still doesn't work? Manual, expert-run attacks can be too difficult or expensive to perform in practice. Or they might not give us enough reliable signal. What should we do then?

Final step: Make a judgment call

The next question we need to face is: what is the alternative? If we don't deploy our DP algorithm with a large privacy budget, what do we do instead?

In practice, the answer is rarely "the data does not get published or shared". Rather, organizations fall back on ad hoc anonymization techniques, like \(k\)-anonymity. And if such an alternative method provides acceptable levels of utility… they may decide that this is better than DP with a large budget that would reach a similar accuracy.

But this is strictly worse! I'd rather have a large privacy budget than an infinite one! Having some provable guarantees is better than not estimating risk in a principled way!

This is an opinionated philosophical stance. Even if we set it aside, though, DP is also a better option in practice for privacy protection. I see three main reasons why.

1. Empirically, DP provides surprisingly good protections against practical attacks, even with large \(\varepsilon\) values. This seems to be true both for machine learning models and for statistical data products. Researchers don't fully understand why, but this what their (limited) data is telling them so far. By contrast, ad hoc anonymization methods keep being badly broken.
2. Say we deployed a DP mechanism with a large \(\varepsilon\), and we later realize that it is vulnerable to a practical attack. How much do we need to change our deployment to mitigate the risk? Barring major implementation issues, adjusting the privacy parameters is likely to be enough: if we lower the \(\varepsilon\) enough, the formal guarantees will kick back. So we'll only need to re-evaluate trade-offs, and change parameters. The same cannot be said for ad hoc methods like \(k\)-anonymity: a differencing attack that works with \(k=20\) won't be mitigated by setting \(k\) to 30 instead. Fixing the flaw would require a much deeper redesign of the privacy strategy.
3. Deploying DP for a real-world use case often has additional, compound privacy benefits. It builds trust in the technology within an organization. It teaches people valuable skills: how to use these techniques, how to reason about worst-case scenarios, how to think about cumulative risk. It encourages the people using the data to learn how to reason about uncertainty. All of this will make it easier to ship the next DP deployment… and maybe manage to use stricter parameters next time!

John Abowd, who served as Chief Scientist of the U.S. Census Bureau, summarizes this pragmatic perspective.

Traditional disclosure limitation frameworks have an infinite privacy loss. The first step in modernizing them is to go from infinite to bounded privacy loss. Then, we can work on lowering it.

Finally, we need to remember that privacy is only ever one part of the story.

Organizations don't publish data because they want to protect it. They do it to fulfill their mission, to address a business problem, or to pursue some other goal. Privacy risk is always weighed against these other considerations. Differential privacy cannot tell you whether what you're doing is a good use of data. It only gives you a way to quantify and control the privacy cost that you incur in doing so. For compelling use cases, weaker privacy guarantees might be a perfectly acceptable cost.

In the real world, privacy-utility trade-off decisions boil down to judgment calls. There's no avoiding it. The best we can do is to openly discuss the choices we make, so we can learn from each other. Over time, we'll have more tools, principles, and best practices, and will be empowered to make better decisions.

So let's get to work!

---

Speaking of getting to work, here are some examples of real-world deployments that illustrate the points in this post.

• Improved privacy accounting. Many academic papers on privacy accounting are directly motivated by practical deployments. Better theorems for composing the exponential mechanism lower the \(\varepsilon\) for LinkedIn's Audience Engagements API. Google's guide to integrating DP in machine learning outlines which amplification results to use depending on the algorithm (Table 3). A recent update to my list of real-world deployments provides a even simpler example: I started using a tighter conversion formula from zero-concentrated DP to \((\varepsilon,\delta)\)-DP… and a bunch of reported \(\varepsilon\) values got smaller as a result!
• Fine-grained privacy analysis. In Facebook's Full URLs Data Set (page 11), the authors analyze the privacy loss in two steps. First, they quantify it for each kind of social network interaction. Then, they translate it to a user-level guarantee, which depends on how many interactions each user contributed. The U.S. Census Bureau also used this approach in the 2020 Decennial Census: they quantified the privacy loss per person, but also per demographic attribute (Section 8 of this paper).
• Empirical attacks. The most prominent example is probably the one from the U.S. Census Bureau. It informed not only the initial decision to use differential privacy, but the privacy parameters used in production as well. LinkedIn also reports using an empirical attack to set the privacy parameters for their Single Post Analytics deployment.

If you know of another one, let me know!

---

I am extremely grateful to Philip Leclerc and Ryan Rogers for their excellent feedback and suggestions on drafts of this post, and to John Abowd for providing me with the quote. Thanks as well to Marc Jeanmougin and Callisto for their helpful comments.