Lowering the cost of anonymization

4.2.3 System model and design

In this section, we present an overview of the design of our framework, detail the building blocks necessary to implement it, and formally define it as an operator in relational algebra. We finish by providing a proof that the entire process provides user-level differential privacy.

Overview

As suggested in Section 4.2.1, we assume that there is a special column of the input dataset that specifies which user owns each row. The system is agnostic to the semantics of this special column. In principle, it can be any unit of privacy that we need to protect: a device identifier, an organization, or even a unique row ID if we want to protect rows and not users. For simplicity of notation we assume that this special column is a user identifier. Users may own multiple rows in each input table, and each row must be owned by exactly one user. Our model guarantees $(ε, δ)$ -DP with respect to each user, as defined in Definition 79.

Our DP query engine uses the underlying SQL engine to track user ID metadata across tables, and invokes a DP query rewriter when our anonymization query syntax is used on tables containing user data and any applicable permission checks succeed. Listing 4.5 provides an example of a SQL query accepted by our system.

 
SELECT WITH ANONYMIZATION 
  T1.partition_key, 
  ANON_SUM(T2.val, 0, 1) 
FROM Table1 T1 JOIN Table2 T2 USING(uid) 
GROUP BY T1.partition_key

Listing 4.5: Anonymization query example

The query rewriter decomposes such queries into two stages, one before and one after our introduced DP aggregation operator, invoked with SELECT WITH ANONYMIZATION.

The first stage begins by validating that all table subqueries inside the DP operator’s FROM clause enforce unique user ownership of intermediate rows, which is informally described in Section 4.2.3. Next, for each row in the subquery result relation, our operator partitions all input rows by the vector of user-specified GROUP BY keys and the user identifier, and applies an intermediate non-private SQL aggregation to each group. For example, for ANON_SUM, we use SUM as a partial aggregation. Adjusting query semantics in this way is necessary to ensure that, in the next stage, the cross-user aggregations of each partition receive only one input row per user, this is described in Section 4.2.3.

For the second stage, we sample a fixed number of these partially aggregated rows for each user to limit user contribution across partitions, which is described in Section 4.2.3. We then compute a cross-user DP aggregation across all users contributing to each GROUP BY partition, limiting user contribution within partitions; this is described in Section 4.2.3. Finally, we randomly drop certain partitions that contain too few users, to guarantee that the list of published partitions does not break differential privacy guarantees, a process described in Section 4.2.3.

The full process is formalized in Section 4.2.3, where we define our operator in the language of relational algebra.

Allowed subqueries

SQL queries can, in principle, contain subqueries that perform arbitrary transformations on the input tables. However, for our framework to guarantee differential privacy, we need to limit this capability: we need the concept of row ownership to stay relevant throughout the computation, and be able to determine which row of the subquery output belongs to which user in the input dataset.

Thus, the relational operators present in the subquery must not create any intermediate objects of shared ownership: no intermediate row may be derived from rows owned by different users. A naive application of certain relational operators violate this requirement. For example, for the aggregation operator, rows owned by distinct users may be aggregated into the same partition. Then the resulting row from that partition will be owned by all users whose data are contributed to the group. For the naive join operator, two rows from distinct users may be joined together, creating a row owned by both users.

This restriction limits our system since some queries cannot be run. We observed that in practice, most use-cases can be fit within these constraints, and leave extensions to a wider class of queries for future work. This might require a different model than the one presented here, but changing query semantics will always be necessary for queries with unbounded sensitivity.

Assume that the column containing user identifier is named uid. We address the shared ownership issue by restricting each operator composing the subquery such that, for each row in that operator’s output relation, that row is derived only from rows in the input relation that have matching uid attributes. We enforce this rule for aggregate operators by requiring that the analyst additionally groups-by the input relation’s uid attribute. For join operators, we require that the analyst adds a USING(uid) clause (or equivalent) to the join condition. Additionally, each operator of $T$ must propagate uid from the input relation(s) to the output relation. In queries where this is unambiguous (i.e., the analyst does not refer to uid in the query), we can automatically propagate uid.

A formalization of this approach, which list alternatives for each basic operator, is listed in Table 4.3, in Section 4.2.3. They are enforced recursively during the query rewrite for each operator that composes the subquery.

Per-user aggregation

First, we aggregate the data of each user per-partition, using the non-private version of the aggregator in the original query. For example, for ANON_SUM, we use the SUM SQL operator to sum all contributions of each user in each partition.

This operation guarantees that in the cross-user aggregation stage, each user contributes at most once to each aggregation. This does come at the cost of introducing another semantic change to the original query. For example, for ANON_AVG, we end up computing the average of per-user averages, which could be completely different from the real average of all values. It is easy to create examples of data distributions in which this difference has a large impact; however, we observed that it does not seem to introduce significant bias in practical applications.

This step also limits the type of aggregations that can be performed within our framework: for example, we cannot easily implement ANON_COUNT(DISTINCT col) when col is different from uid as the per-user aggregation would not contain enough information to combine the contributions of multiple users (as col values need to be de-duplicated to preserve semantics). We come back to these considerations in Section 4.3.1.

Stability bounding

Next, to bound the total privacy budget of the computation, we need to ensure that each user contributes to a fixed number of partitions in the output row. To this end, we adapt the notion of query stability from [McS09].

Definition 81 (Global stability). Let $T$ be a function $T : D \to D$ . We say that $T$ is $c$ -stable if for all $D_{1}, D_{2} \in D$ :

∥ T (D_{1}) - T (D_{2}) ∥ \leq c ∥ D_{1} - D_{2} ∥ .

As an immediate consequence, if a user $i d$ owns $k$ rows in $D$ , and $T$ is a $c$ -stable transformation, then there are at most $k \cdot c$ rows derived from rows owned by $i d$ in $T (D)$ .

Our privacy model requires the input to the cross-user aggregation to have constant stability. Simple SQL operators have a stability of one: for example, each record in an input relation can only be projected onto one record. An addition or a deletion can only affect one record in a projection, so projections have a stability of one. The same logic applies for selection.

Other operators, such as joins, have unbounded stability because source records can be multiplied. Adding or removing a source record can affect an unbounded number of output records. When SQL operators are sequentially composed, we multiply the stability of each operator to yield the entire query’s overall stability. Thus, even a subquery accepted by the checks of Section 4.2.3 might not be $c$ -stable for any $c$ .

To fix this problem, we can compose an unbounded transform $T$ with a stability-bounding transform $T_{κ}$ to yield a composite $κ$ -stable transform:

∥ T_{κ} (T (D_{1})) - T_{κ} (T (D_{2})) ∥ \leq κ ∥ D_{1} - D_{2} ∥ .

To define $T_{κ}$ , we use partitioned-by-user reservoir sampling with a per-partition reservoir size of $κ$ , which has a stability of $κ$ . Reservoir sampling was chosen for its simplicity, and because it guarantees a strict bound on the contribution of one user. Non-random sampling (e.g. taking the first $κ$ elements, or using systematic sampling) risks introducing bias in the data, depending on the relative position of records in the dataset. Simple random sampling does not guarantee contribution bounding, and all types of sampling with replacement can also introduce bias in the data.

Joins appear frequently in queries [JNS18], so it is imperative to support them in order for an engine to be practical. Since joins have unbounded stability, a stability bounding mechanism is necessary to provide global stability privacy guarantees on queries with joins. We can thus support a well bounded, full range of join operators.

Bounded-contribution aggregation

Let us now introduce the set of supported $ε$ -DP statistical aggregates with bounded contribution. These functions are applied after the per-user, per-partition aggregation step discussed in Section 4.2.3, and after the stability bounding operator. Importantly, at this step, we assume that each user’s contributions to a single partition have been aggregated to a single input row; this property is enforced by the query rewriter.

COUNT(DISTINCT uid) is the simplest example of an aggregation with bounded contribution: it counts unique users, so adding or subtracting a user will change the count by no more than 1. For more complex aggregation functions, we must determine how much a user can contribute to the result and add appropriately scaled noise. A naive solution without limits on the value of each row leads to unbounded contribution by a single user. For example, a SUM which can take any real as input has an unbounded $L^{1}$ -sensitivity (see Definition 80).

To address this, each $ε$ -DP function accepts an additional pair of lower and upper limit parameters $L$ and $U$ used to clamp (i.e., bound) each input. For example, consider the anonymized sum function ANON_SUM(col, $L$ , $U$ ).

Let ${sum}_{L}^{U} : D \to R$ be the function that transforms each of its inputs $x$ into $x^{'} = max (min (x, U), L)$ , and then sums all $x^{'}$ . The global sensitivity for this bounded sum function is:

Δ {sum}_{L}^{U} = max (| L |, | U |)

and thus, ANON_SUM can be defined by using this function and then adding noise scaled by this sensitivity. A special case of ANON_SUM, widely used in practice, is ANON_COUNT, which is equivalent to summing 1 for each record present in the dataset.

Once the sensitivity is bounded, noise is added to internal states using the well-known Laplace mechanism (see Section 2.1.6) before a differentially private version of the aggregate result is released.

For ANON_AVG, we use the Algorithm 2.4 from [LLSY16] (Section 2.5.5): we take the quotient of a noisy sum (bounded as in ANON_SUM, and scaled by sensitivity $| U - L | ∕ 2$ ) and a noisy count. ANON_VAR is similarly derived; we use the same algorithm to compute a bounded mean and square it, and to compute a mean of bounded squares. ANON_STDDEV is implemented as the square root of ANON_VAR.

ANON_NTILE, which returns a given percentile of values given as input, is currently based on a Bayesian binary search algorithm [BOH08, KK07], and can be used to define ANON_MIN, ANON_MAX, and ANON_MEDIAN. The upper and lower bounds are only used to restrict the search space and do not affect sensitivity. At each iteration of the internal binary search, we count the number of values below and above the target value, add noise to these two counts, and determine the next step of this binary search based on these counts. Importantly, this requires to keep all elements in memory, which does not scale to very large input data. A simple solution, which we implemented, is to randomly sample input values once we reach a memory limit. Further research is currently underway to find better options.

For the rest of this section, we assume that contribution bounds are specified as literals in each query to simplify our presentation. Setting bounds requires some prior knowledge about the input set. For instance, to average a column of ages, the lower bound could be reasonably set to $0$ and the upper bound to $120$ . To enhance usability in the case where there is no such prior knowledge, we also introduce a mechanism for automatically inferring contribution bounds, described in more detail in Section 4.2.5.

Table 4.2 lists our suite of aggregate functions. For each function that can be implemented using other functions, we give the equivalent formulation. Note that the equivalent formulation is given using SQL for simplicity, but we do not always implement it via SQL rewriting; we sometimes implement them as standalone low-level aggregators and only reuse the code for other aggregators. We come back to these implementation considerations in Section 4.3.1.

Function	Equivalent formulation
ANON_SUM(col, L, U)
ANON_COUNT(col, U)	ANON_SUM(1, 0, U)¹
ANON_COUNT(DISTINCT uid)	ANON_COUNT(uid, 1)
ANON_AVG(col, L, U)	²
ANON_VAR(col, L, U)	ANON_SUM(colcol, 0, MAX(LL,U*U)) - ANON_SUM(col, L, U)^2³
ANON_STDDEV(col, L, U)	SQRT(ANON_VAR(col, L, U))
ANON_NTILE(col, ntile, L, U)	⁴
ANON_MIN(col, L, U)	ANON_NTILE(col, 0, L, U)
ANON_MAX(col, L, U)	ANON_NTILE(col, 1, L, U)
ANON_MEDIAN(col, L, U)	ANON_NTILE(col, 0.5, L, U)

¹ Technically, ANON_SUM(IF col IS NOT NULL THEN 1 ELSE 0, 0, U).
² This could be formulated as ANON_SUM(col, L, U) / ANON_COUNT(col, U’)for a well-chosen U’. However, the choice of U’makes this option undesirable, so we implement ANON_AVGseparately instead; see the extended discussion in Section 4.3.1.
³ Note that the per-user aggregation step for ANON_VARis not VAR; we give more details about this case in Section 4.3.1.
⁴ We discuss this aggregation in more detail in Section 4.3.1.

Table 4.2:

ε

-DP aggregate functions

Minimum user threshold

In this section, we outline a technique proposed in [KKMN09] to prevent the presence of arbitrary partitions (GROUP BY keys) in a query from violating the privacy predicate: the $τ$ -thresholding mechanism. For example, consider the naive implementation in Listing 4.6.

 
SELECT col1, ANON_SUM(col2, L, U) 
FROM Table 
GROUP BY col1

Listing 4.6: Leaking GROUP BY keys

Suppose that for the value col1 = c, only one user $i d$ contributed to the sum. Then querying without data from $u$ would reveal the absence of the output row corresponding to group col1 = c. It would be revealed with certainty that user $u$ has value $c$ for col1.

To prevent this, for each result aggregation row, we calculate an $ε$ -DP count of unique contributing users. If that count is less than some minimum user threshold $τ$ , the result row is discarded. $τ$ is chosen by our model based on $ε$ , $δ$ , and $κ$ parameter values. In the example above, the output row for group col1 = c would only appear in the result if noise added to the total user count (1) would result in a value larger than $τ$ : this only happens with fixed probability, which we can control by carefully chosing $τ$ .

The choice of $τ$ depends on $ε$ , $δ$ , and $κ$ ;

Theorem 12. Let $ε, δ, κ > 0$ . Define

τ = 1 - \frac{κ ln (2 - 2 {(1 - δ)}^{1 ∕ κ})}{ε} .

If an SQL query:

guarantees that each user appears in at most $κ$ partitions;
for each partition, computes and releases an $ε ∕ κ$ -DP noisy count of the number of contributing users using the Laplace mechanism;
does not release anything for empty partitions;
and only releases counts greater or equal than $τ$ ;

then it provides user-level $(ε, δ)$ -DP.

Proof. First, note that that if a dataset $D$ contains a single row, then the probability that an $ε$ -DP noisy count of the number of rows in $D$ will yield at least $τ$ for any $τ \geq 1$ is

ρ_{τ} = \frac{1}{2} e^{- (τ - 1) ε} .

Indeed, this is a special case of Section 5.2 in [KKMN09]: the noisy count is distributed as the Laplace distribution centered at the true count of $1$ with scale parameter $1 ∕ ε$ . Evaluating the CDF at $τ$ yields $ρ_{τ}$ .

Let us now prove the main statement. Let $M$ be the SQL operation described in the theorem. Consider any pair of datasets $D_{1}, D_{2}$ such that ${∥ D_{1} - D_{2} ∥}_{u} = 1$ and such that the set of non-empty groups from $D_{1}$ is the same as that for $D_{2}$ ; call this set $G$ . The $ε ∕ κ$ -DP noisy count will get invoked for all groups in $G$ for both datasets, and the $τ$ -thresholding applied. For all groups not in $G$ , no row will be released for both datasets. A change in the user may affect a maximum of $κ$ output counts, each of which is $ε ∕ κ$ -DP, so by the composition property of differential privacy (see Proposition 5), we have:

P [M (D_{1}) \in S] \leq e^{ε} P [M (D_{2}) \in S]

Next, consider an empty dataset $D_{3}$ . Let $U$ be the set of all outputs and let $E$ be the output set containing only the output “no result rows are produced”. Then we have $P [M (D_{3}) \in U ∖ E] = 0$ . It remains to show that for dataset $D_{4}$ containing a single user, $P [M (D_{4}) \in U ∖ E] \leq δ$ . The $ε$ -DP count is computed by counting the number of rows, and then adding Laplace noise with scale $κ ∕ ε$ . Dataset $D_{4}$ contains values for a maximum of $κ$ groups; it is only possible to produce an output row for those groups. For each groups, the probability that the noisy count will be at least $τ$ is $ρ_{τ} = \frac{1}{2} e^{- \frac{(τ - 1) ε}{κ}}$ , by the initial observation. Then:

P [M (D_{4}) \in E] = 1 - {(ρ_{τ})}_{τ}^{κ}

so we need to satisfy:

P [M (D_{4}) \in U ∖ E] = {(ρ_{τ})}_{τ}^{κ} \leq δ .

Solving for $τ$ in the expression ${(ρ_{τ})}_{τ}^{κ} \leq δ$ :

τ \geq 1 - \frac{κ ln (2 - 2 {(1 - δ)}^{1 ∕ κ})}{ε} .

Lastly, consider SQL engine operator $f$ and datasets $D_{5}, D_{6}$ such that $D_{6}$ is $D_{5}$ with the addition of a single user. It remains to consider the case where $D_{5}$ and $D_{6}$ do not have the same set of non-empty groups. Since they differ by one user, $D_{6}$ may have a maximum of $κ$ additional non-empty groups, each containing $1$ unique user; call this set of groups $G$ . Call the set of the remaining groups $G^{'}$ . Split the rows of $D_{5}$ into two datasets: the rows that correspond to groups in $G$ and $G^{'}$ , respectively. Call the rows of $D_{6}$ that correspond to groups $G$ as $D_{6}^{0}$ and the rows that correspond to groups $G^{'}$ as $D_{6}^{1}$ . Note that $D_{5}$ only contains rows corresponding to groups $G^{'}$ . Now, split the operator $f$ into two operators $f_{0}$ and $f_{1}$ : $f_{0}$ is $f$ with an added filter that only outputs result rows corresponding groups in $G$ ; $f_{1}$ is the same for $G^{'}$ .

We have decomposed our problem into the previous two cases. The system of $f_{0}$ , $D_{5}$ , and $D_{6}^{0}$ is the case where the pair of datasets have the same set of non-empty groups, $G^{'}$ . The system of $f_{1}$ , the empty dataset, and $D_{6}^{1}$ is the case where the non-empty dataset contains a single user. Each system satisfies the DP predicate separately. Since they operate on a partition of all groups in $D_{5}$ and $D_{6}$ , the two systems satisfy the DP predicate when recombined into $f$ , $D_{5}$ , and $D_{6}$ .

We have shown that for two datasets differing by a single user, the DP predicate is satisfied. Thus, we have shown that our SQL query provides user-level $(ε, δ)$ -DP. □

Note that this operation must be taken into account as part of privacy budget computation. If the only operation that the user requested was ANON_COUNT(DISTINCT uid), then we can simply post-process the results of this noisy aggregation to threshold the output. Otherwise, we have to add this aggregation alongside the requested ones in the query rewriter, and split the budget between all these operations.

Query semantics

In this section, we formally define our $(ε, δ)$ -DP relational operator, denoted by $χ$ , using some of the conventional operators in relational algebra. This is simply a reformulation than the process described in Section 4.2.3 so far.

First, let us quickly recall standard operators in relational algebra, used to describe the transformations on datasets that occur in a query.

$Π_{s} (R)$ : project columns $s$ from $R$ .
$σ_{φ} (R)$ : select from $R$ satisfying the predicate $φ$ .
$_{g} G_{a} (R)$ : group on the cross products of distinct keys in the columns in $g$ ; apply the aggregations in $a$ to each group.
$R ⋈_{θ} cond S$ : take the cross product of rows in $R$ and $S$ , and select only the rows that satisfy the predicate $cond$ .

Let $s$ (select-list), $g$ (group-list), and $a$ (aggregate-list) denote the attribute names $s_{1}, \dots, s_{i}$ , $g_{1}, \dots, g_{j}$ , and $a_{1}, \dots, a_{k}$ , respectively. Assume $a$ is restricted to only contain the $ε$ -DP aggregate function calls discussed in Section 4.2.3. Our introduced operator, $_{g} χ_{a}$ , can be interpreted as an anonymized grouping and aggregation operator with similar semantics to $_{g} G_{a}$ , and supports queries in the general form given in Listing 4.7.

 
SELECT WITH ANONYMIZATION  $s$ ,  $a$  
FROM  $T$ (R) 
GROUP BY  $g$

Listing 4.7: Generic form of the queries supported by our relational operator

χ

First, $χ$ verifies row ownership constraints on $T$ : it must not contain any additional analyst-specified operators which create intermediate objects of shared ownership, as defined in Section 4.2.3. Formally, $χ$ imposes that all operators present in this subquery are allowed, as defined by Table 4.3.

Operator	Basic form	Required variant
Projection	$Π_{a} (R)$	$Π_{u i d, a} (R)$
Selection	$σ_{φ} (R)$	$σ_{φ} (R)$
Aggregation	$_{g} G_{a} (R)$	$_{u i d, g} G_{a} (R)$
Join	$R ⋈_{θ} cond S$	$R ⋈_{θ} cond \land R . u i d = S . u i d S$

Table 4.3: Allowed table subquery operators

If $R$ is an input table where each row is owned by exactly one user, and $T$ satisfies those constraints, then this guarantees that $T (R)$ also has such a user identifier uid in its schema. We can then use $T (R)$ as the input to our proposed operator $χ$ , and define our query $Q$ :

Q = Π_{s} (_{g} χ_{a} (T (R)))

The query rewriter discussed in Section 4.2.3 transforms a query containing $χ$ into a query that only contains SQL primitives, minimizing the number of changes to the underlying SQL engine. We define the following in order to express our rewriting operation.

Let $# u i d$ denote the number of user IDs present in a given partition. In SQL, it would be expressed as COUNT(DISTINCT uid). We use it in the condition $# u i d \geq τ$ , which captures the $τ$ -thresholding mechanism introduced in Section 4.2.2 and discussed in more detail in Section 4.2.3.
Let $a^{'}$ be the corresponding non- $ε$ -DP partial aggregation functions of $a$ . For example, if $a$ is ANON_SUM, $a^{'}$ would be SUM.
Let $_{m} T_{n}$ behave like a reservoir-sampling SQL TABLESAMPLE operator where $m$ is the grouping list and $n$ is the number of samples per group. In other words, the operation $_{m} T_{n} (R)$ partitions $R$ by columns $m$ . For each partition, it randomly samples up to $n$ rows. We use $T$ as this stability-bounding operator, discussed in Section 4.2.3.

When the query rewriter is invoked on the following relational expression $Q$ containing $χ$ :

Q = Π_{s} (_{g} χ_{a} (T (R)))

it returns the modified expression, with $χ$ expanded:

\begin{matrix} U & = Π_{u i d, g, a^{'}}^{'} (_{u i d} T_{κ} (_{u i d, g} G_{a^{'}}^{'} (T (R)))) S & = Π_{s} σ_{# u i d \geq τ} (_{g} G_{# u i d, a} (U)) \end{matrix}

Effectively, the rewriter splits $Q$ into the two-stage aggregation $U$ and $S$ .

$U$ groups the output of $T (R)$ by the key vector $(u i d, g)$ , applying the partial aggregation functions $a^{'}$ to each group. $κ$ rows are then sampled for each user. The first aggregation enforces that there is only one row per user per partition during the next aggregation step.
$S$ performs a second, differentially private, aggregation over the output of $U$ . This aggregation groups only by the keys in $g$ and applies the $ε$ -DP aggregation functions $(f (u i d), a)$ . These functions assume that every user contributes at most one input row. A filter operator is applied last to suppress any rows with too few contributing users.

Together, this implements the process described in the previous parts of Section 4.2.3.

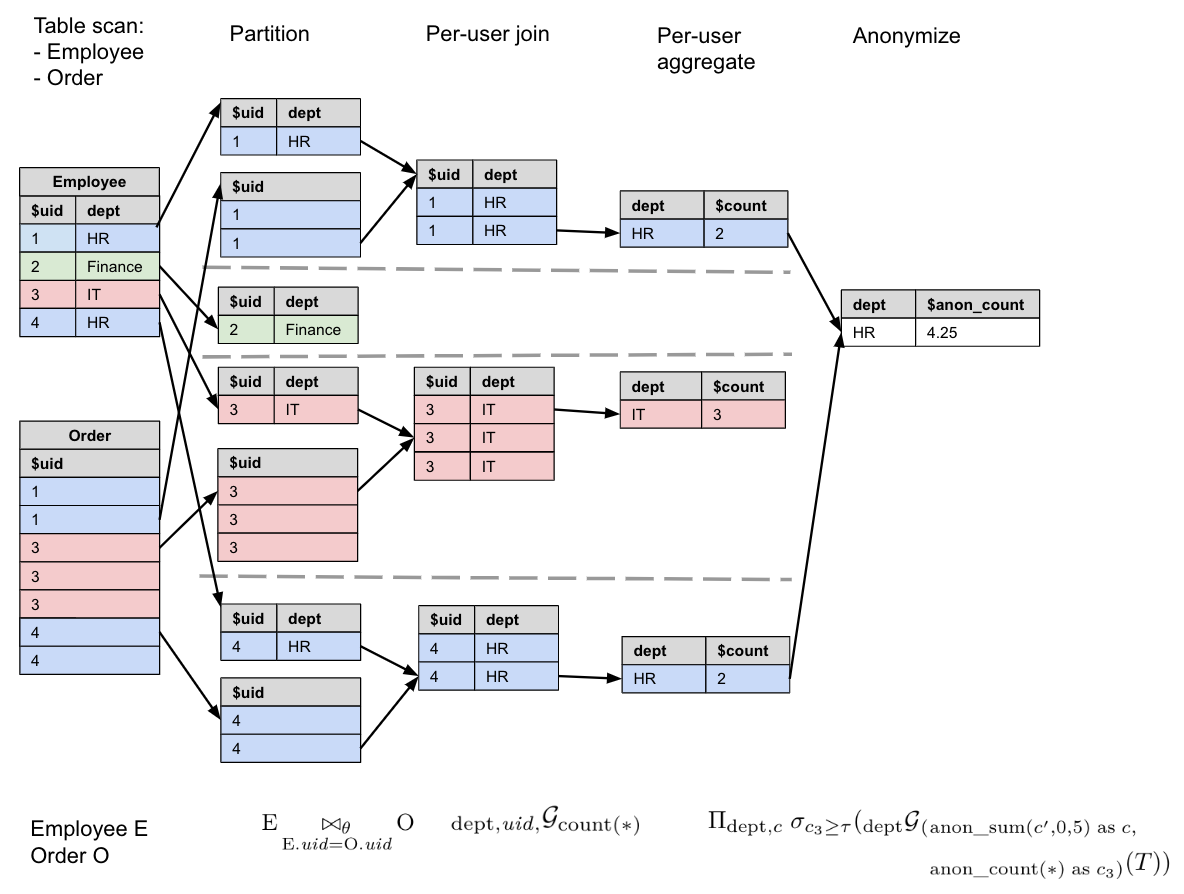
Let us illustrate this process with a concrete example. Consider the following query. It assumes we have an Employee table and an Order table, which both have a $u i d$ field, and it is counting the number of orders made by employees in each department.

 
SELECT WITH ANONYMIZATION 
  dept, ANON_COUNT(*, 5) AS c 
FROM Employee E JOIN Order O USING(uid) 
GROUP BY dept

Listing 4.8: Anonymization query containing a simple join.

Recall that ANON_COUNT(*, U) is equivalent to ANON_SUM(col, 0, U) in the cross-user aggregation step. We can express this query in relational algebra using our DP operator $χ$ :

Q = Π_{dept, c} (_{dept} χ_{ANON_COUNT(*, 5) AS c} (E ⋈_{θ} E . u i d = O . u i d O))

Let us expand $χ$ into the two-stage aggregation, $U$ and $S$ , and let us call $T$ the initial table subquery. Our query can then be written as:

\begin{matrix} T & = Π_{dept, u i d, c_{2}} (_{dept, u i d} G_{COUNT(*) AS c_{2}} (E ⋈_{θ} E . u i d = O . u i d O)) U & = Π_{dept, u i d, c_{2}} (_{u i d} T_{κ} (U)) S & = Π_{dept, c} σ_{c_{3} \geq τ} (_{dept} G_{ANON_SUM (c^{'}, 0, 5) AS c, ANON_COUNT(*) AS c_{3}}^{'} (T)) \end{matrix}

Note that we add an additional user counting $ε$ -DP function, aliased as $c_{3}$ , which is compared to our threshold parameter, $τ$ , to ensure that the grouping does not violate the $(ε, δ)$ -DP predicate, to be discussed in Section 4.2.3. In this case $c_{3}$ is the number of unique users in each department: as each user contributes at most 1 to each partition, we can simply use ANON_COUNT(*) to compute this count of unique users.

In Figure 4.9, we illustrate the workflow with example tables Employee and Order, $τ = 2$ , and $κ = 1$ .

Figure 4.9: Example workflow of anonymized query. Note that in the last step, the IT department gets dropped from $τ$ -thresholding.

User-level differential privacy

In this section, we show that our engine satisfies user-level $(ε, δ)$ -DP, as defined in Section 4.2.1.

Suppose that a query $M$ has aggregate function list $a = a_{1}, \dots, a_{N}$ , and grouping list $g = g_{1}, \dots, g_{J}$ . Let the privacy parameter for aggregation function $a_{i}$ be $ε_{i}$ .

Consider any set of rows owned by a single user in the input relation of our anonymization operator, $_{g} χ_{a}$ . We first partition and aggregate these rows by the key vector $(u i d, g)$ , before sampling up to $κ$ rows for each partition by $u i d$ .

The result for a group $j$ is reported if the $τ$ -thresholding predicate defined in Section 4.2.3 is satisfied. Computing and reporting the comparison count for this predicate is $ε_{j}^{'}$ -DP. For $D_{1}, D_{2} \in D$ , such that they differ by a user’s data for a single group $j$ , consider each aggregation function $a_{i}$ as applied to group $j$ . By composition theorems and Theorem 12, we provide $(ε_{j}^{'} + \sum ε_{i}, δ_{j})$ user-level $(ε, δ)$ -DP for that row.

However, there are many groups in a given query. Due to our stability bounding mechanism, a single user can contribute to up to $κ$ groups. The $κ$ output rows corresponding to these groups can be thought of as the result of $κ$ sequentially composed queries. Let $D_{1}, D_{2} \in D$ such that ${∥ D_{1} - D_{2} ∥}_{u} = 1$ . Let $ε$ be the sum of the $κ$ greatest elements in the set ${ε_{j}^{'} + \sum ε_{i}}_{j = 1, \dots, J}$ . Again, by composition, we conclude that for any output set $S$ , and some $δ > 0$ , we have

P [M (D_{1}) \in S] \leq e^{ε} P [M (D_{2}) \in S] + δ

This shows that given engine-defined parameters $ε$ , $δ$ , and $κ$ , it is possible to set privacy parameters for individual $ε$ -DP functions to satisfy the query $(ε, δ)$ -DP predicate. For example, we can set $ε_{j}^{'}$ and $ε_{i}$ to $\frac{ε}{κ (N + 1)}$ for all $i$ and $j$ . $δ$ is enforced by the derived parameter $τ$ as discussed in Section 4.2.3. Both user-privacy parameters $ε$ and $δ$ can therefore be bounded to be arbitrarily small by analysts and data owners.

Note that the method we use to guarantee user-level differential privacy can be interpreted as similar to row-level group privacy: after the per-user aggregation step, we use the composition theorem to provide group privacy for a group of size $κ$ . Alone, row-level group privacy does not provide user-level privacy, but in combination to user-level contribution bounding, this property is sufficient to obtain the desired property.

LINKPREV LINKUP LINKNEXT