Lowering the cost of anonymization

3.1.2 Correlated data

When data is correlated, dependencies create problems for privacy definitions that assume an attacker with partial knowledge. To illustrate this, we recall two previously introduced definitions that model this situation differently: noiseless privacy (NPr) and distributional differential privacy (DistDP). We show that both definitions have undesirable consequences when data is correlated, and use DistDP as a starting point to solve this problem in two steps. First, we modify DistDP and introduce a new definition, causal differential privacy (CausDP), to prevent its most direct problems. Second, we propose a criterion that encompasses many use-cases but avoids known issues with correlated data, and makes CausDP equivalent to NPr. This allows us to cleanly define a rigorous notion of DP with partial knowledge, which allows for many practical use cases, but avoids the known issues with correlated data.

Note that there has been substantial debates about the impact of correlations on the guarantees that DP provides. The debates are summarized in [368], where the authors suggest a possible resolution: interpreting DP as a causal property. In this section, we continue this line of work in the context of partial knowledge. In particular, we show that modifying the definition in the same way as the “causal variants” of [368] is not sufficient to solve all issues created by the presence of correlations in the data, when the attacker only has partial knowledge.

For simplicity, in this section, we only consider the case with $δ = 0$ . We re-introduce $δ > 0$ in Section 3.1.3.

Existing notions

The assumption that the attacker lacks background knowledge can be represented by considering the input data to be noisy. This idea was first proposed in [116], and was formalized in [46] as noiseless privacy. Instead of comparing two databases that differ in only one record, it uses a probability distribution $θ$ , conditioned on the value of one record $D (i)$ : the randomness in $θ$ captures the attacker’s uncertainty. This probability distribution generates not only a dataset $D$ but also the attacker’s partial knowledge $B$ (with values in some space $B$ ). For brevity, we abbreviate $P_{(D, B) \sim θ}$ as $P_{θ}$ , abbreviate the observation $D = ˆ D$ by $ˆ D$ , and the observation $B = ˆ B$ by $ˆ B$ ; these notations as well as others used in this paper are summarized in the notation table on page 32.

Definition 49 ( $(Θ, ε)$ -noiseless privacy [46]). Given a family $Θ$ of probability distribution on $D \times B$ , a mechanism $M$ is $(Θ, ε)$ -noiseless private (NPr) if for all $θ \in Θ$ , all $ˆ B \in B$ , all indices $i$ and all $t, t^{'} \in T$ such that $P_{θ} [ˆ B, D (i) = t] \Leftrightarrow 0$ and $P_{θ} [ˆ B, D (i) = t^{'}] \Leftrightarrow 0$ (we call this condition “ $ˆ B$ is compatible with $D (i) = t$ and $D (i) = t^{'}$ ”):

M {(D)}_{| θ, ˆ B, D (i) = t} \approx_{ε} M {(D)}_{| θ, ˆ B, D (i) = t^{'}}^{'} .

Here, the notation $M {(D)}_{| θ, ˆ B, D (i) = t}$ refers to the random variable defined by $M (D)$ , where $D \sim θ$ , conditioned on the event “ $B = ˆ B$ and $D (i) = t$ ”.

Note even though we make the attacker’s partial knowledge $ˆ B$ explicit, we could simplify the definition to not mention it explicitly. Indeed, for each distribution $θ \in Θ$ with values in $D \times B$ , we could simply take all possible background knowledges $ˆ B$ generated by $θ$ , and consider the family of distributions $θ_{| ˆ B}$ , which only generate a dataset $D$ . We use this conceptual simplification in Definition 33 and Definition 34, in Section 2.2.5. This simplification is no longer possible if we use $(ε, δ)$ -indistinguishability with $δ > 0$ , as we show in Section 3.1.3.

The original intuition behind DP states that changing one record must not change the output too much. NPr attempts to capture this intuition for an attacker with partial knowledge, but Bassily et al. [36] argue that this definition is too strong. The following example illustrates their argument.

Example 1. Assume $θ$ has a global parameter $μ$ that is either +1 or -1 with equal probabilities, and outputs $n$ normally distributed records with mean $μ$ and a small standard deviation. Releasing the average of the record values is not NPr: for all indices $i$ , $M {(D)}_{| θ, D (i) = 1}$ will be close to $1$ and $M {(D)}_{| θ, D (i) = - 1}$ will be close to $- 1$ , so the two distributions are very distinguishable. This happens even though the impact of a single record in the database is low: once $μ$ is fixed, the random choice of $i$ is unlikely to have a large effect on the global average.

This example shows a definitional problem. If the attacker previously knows $μ$ , revealing $M (D)$ does not give much additional information on the target $D (i)$ : an attacker with less initial knowledge is considered more powerful. We study this in detail in Section 3.1.2.0.

The authors propose an alternative definition to fix this problem: $(Θ, ε)$ -distributional differential privacy. It requires that $M$ can be simulated by another mechanism $Sim$ , that does not have access to the sensitive property. The intuition is as follows: if $M (D)$ is close to $Sim (D_{- i})$ for some simulator $Sim$ , then $M$ cannot leak “too much” about the value of $D (i)$ .

Definition 50 ( $(Θ, ε)$ -distributional differential privacy [36]). Given a family $Θ$ of probability distributions on $D \times B$ , a mechanism $M$ satisfies $(Θ, ε)$ -distributional differential privacy ( $(Θ, ε)$ -DistDP) if there is a simulator $Sim$ such as for all probability distributions $θ \in Θ$ , all $ˆ B \in B$ , all $i$ , and all $t \in T$ such that $ˆ B$ is compatible with $D (i) = t$ :

M {(D)}_{| θ, ˆ B, D (i) = t} \approx_{ε} Sim {(D_{- i})}_{| θ, ˆ B, D (i) = t},

where $D_{- i}$ is the database $D$ from which the record $i$ has been removed.

The distribution $θ$ and the mechanism $M = avg$ from Example 1 satisfy this definition: the simulator can be defined as simply running $M$ on $D_{- i}$ , possibly after adding $+ 1$ or $- 1$ depending on the other records.

Distributional differential privacy under correlations

This critique of NPr is similar to the critique of the associative view of DP in [368]. But the proposed fix has a flaw: $Sim$ can use strong dependencies in the data to artificially satisfy the definition. In the following example, the values of different records are strongly correlated, and the simulator cheats by using these correlations: consequently, the identity function is considered private!

Example 2. Let $θ$ output $n$ duplicate records: for all $i < n$ , $D (2 i)$ is picked from some probability distribution $R$ , and $D (2 i + 1) = D (2 i)$ . Then the identity function $Id$ , which simply outputs its input without any noise, is $({θ}, 0)$ -DistDP! Indeed, the simulator can simply replace the missing record by its duplicate and output the entire database: $Id (D)$ is exactly the same as $Sim (D_{- i})$ .

Here, the dependency relationships are “extreme”, as each record is duplicated. But even when records are less strongly correlated, the problem is still present. In fact, the more dependencies are in the data, the more accurately the simulator can simulate the missing record, and the more “private” the mechanism is (since $ε$ gets lower): a more powerful adversary, who can exploit dependencies in the data, is considered weaker by the definition. This is clearly undesirable.

How can we formalize an adversary that cannot “cheat” using dependencies in the data? We propose one possible option: using the same technique as the causal variants of DP described in [368], we simply change the target record after the distribution is generated.

Definition 51 ( $(Θ, ε)$ -causal differential privacy). Given a family $Θ$ of probability distributions on $D \times B$ , a mechanism $M$ satisfies $(Θ, ε)$ -causal differential privacy ( $(Θ, ε)$ -CausDP) if for all probability distributions $θ \in Θ$ , all $i$ , all $t, t^{'} \in T$ , and all $ˆ B \in B$ compatible with $D (i) = t$ and $D (i) = t^{'}$ :

M {(D)}_{| θ, ˆ B, D (i) = t} \approx_{ε} M {(D_{i \to t^{'}}^{'})}_{| θ, ˆ B, D (i) = t},

where $D_{i \to t^{'}}^{'}$ is the database $D$ , where the $i$ -th record has been replaced by $t^{'}$ .

CausDP still captures DP’s intuition: the change in one data point should not influence the output of the mechanism too much. However, the change happens after the influence of the dependencies in the data. This version is strictly stronger than the original version: if a mechanism $M$ is $(Θ, ε)$ -CausDP, then it is also $(Θ, ε)$ -DistDP. Indeed, the simulator $Sim$ can always replace the missing record with an arbitrary value $b$ and return $M (D_{i \to t^{'}}^{'})$ .

In [36], the authors also introduce an inference-based version of DistDP. We can as easily adapt CausDP to this different formalization.

Definition 52 ( $(Θ, ε)$ -inference-based causal differential privacy). Given a family $Θ$ of probability distributions on $D \times B$ , a mechanism $M$ satisfies $(Θ, ε)$ -inference-based causal differential privacy ( $(Θ, ε)$ -IBCDP) if for all probability distributions $θ \in Θ$ , for all indices $i$ , all $b \in T$ , all $t \in O$ , and all $ˆ B \in B$ compatible with $M (D) = t$ and $M (D_{i \to t^{'}}^{'}) = t$ :

{D (i)}_{| θ, ˆ B, M (D) = t} \approx_{ε} {D (i)}_{| θ, ˆ B, M (D_{i \to t^{'}}^{'}) = t}

where $D_{i \to t^{'}}^{'}$ is the database $D$ , where the record $i$ has been replaced by $b$ .

Note that this definition is equivalent to the indistinguishability-based version (Definition 51) up to a change in parameters.

Proposition 21. $(Θ, ε)$ -CausDP implies $(Θ, 2 ε)$ -IBCDP, and $(Θ, ε)$ -IBCDP implies $(Θ, 2 ε)$ -CausDP.

Proof. The first implication can be proven in the same way as Theorem 1 in [36], replacing $Sim (D_{- i})$ by $M (D_{i \to t^{'}}^{'})$ . For the second implication, suppose that a mechanism $M$ is $(Θ, ε)$ -IBCDP, and assume that the attacker has no background knowledge. Consider an index $i$ , two possible record values $t, t^{'} \in T$ , and one possible output value $O \in O$ . Bayes’ rule gives us:

\begin{matrix} \frac{P [M (D_{i \to t^{'}}^{'}) = O | D (i) = t]}{P [M (D) = O | D (i) = t]} = \frac{P [D (i) = t | M (D_{i \to t^{'}}^{'}) = O]}{P [D (i) = t | M (D) = O]} \cdot \frac{P [M (D) = O]}{P [M (D_{i \to t^{'}}^{'}) = O]} . \end{matrix}

The first term is between $e^{- ε}$ and $e^{ε}$ since $M$ is $(Θ, ε)$ -IBCDP. We only need to show that the second term is also between $e^{- ε}$ and $e^{ε}$ to conclude the proof. Notice that when $D (i) = t^{'}$ , we have $D_{i \to t^{'}}^{'} = D$ . Thus:

\begin{matrix} 1 = \frac{P [M (D_{i \to t^{'}}^{'}) = O | D (i) = t^{'}]}{P [M (D) = O | D (i) = t^{'}]} = \frac{P [D (i) = t^{'} | M (D_{i \to t^{'}}^{'}) = O]}{P [D (i) = t^{'} | M (D) = O]} \cdot \frac{P [M (D_{i \to t^{'}}^{'}) = O]}{P [M (D) = O]} . \end{matrix}

Again, the first term is between $e^{- ε}$ and $e^{ε}$ since $M$ is $(Θ, ε)$ -IBCDP. Since multiplying it with the second term gives $1$ , the second term is also between $e^{- ε}$ and $e^{ε}$ . If the attacker has background knowledge, all the probabilities above are conditioned by $ˆ B$ , and the same reasoning holds.

In the more general case where the attacker does have some partial knowledge, all probabilities above are conditioned by the value of this partial knowledge, and the same reasoning holds. □

This equivalence is only true in the context of this section, where $δ = 0$ ; we explain later why it fails when $δ > 0$ .

Does Example 1 satisfy CausDP? It depends: if $b$ can take arbitrarily large values, $avg (D_{i \to b})$ can be arbitrarily distinguishable from $avg (D)$ . Otherwise, $b$ can only have a bounded influence on the average and $({θ}, ε)$ -CausDP can hold for some $ε$ . In other words, when using the fixed version of the definition, whether a given mechanism is CausDP depends on the sensitivity of the mechanism. This is a good thing: it suggests that it captures the same intuition as DP.

Example 1 shows that CausDP is not stronger than NPr. Is the reverse true? In Example 3, we show that this is not the case.

Example 3. Consider the same $θ$ as for Example 1: it depends on a global parameter, $μ$ , which is either +1 or -1 with equal probabilities, and each of the $n$ records is normally distributed with mean $μ$ and a small standard deviation $σ$ . Let $M$ be the algorithm that counts outliers: it computes the average $˜ μ$ of all data points, and returns the number of records outside $[˜ μ - 5 σ, ˜ μ + 5 σ]$ . As we saw before, conditioning $θ$ on a value of $D (i)$ is approximately equivalent to fixing $μ$ : the number of outliers is going to be the same no matter what (0 with high probability). However, if we first condition $θ$ on $D (i) = t$ , and then change this record into $t^{'}$ , we can choose $t^{'}$ so that this record becomes an outlier; and make it 1 with high probability. Thus, this mechanism is NPr but not CausDP.

Even though Example 3 shows that NPr does not imply CausDP, it is natural to think that in many cases, if you change one data point $D (i)$ as well as all data points correlated with it, it will have a bigger influence on the algorithm that if you only change $D (i)$ without modifying the rest of the data. In Example 4, we show that even for a simple data dependencies and mechanisms, we can find counterexamples to this intuition.

Example 4. Consider a probability distribution $θ$ that outputs $2 n$ records, such as for all $i < n$ , $D (2 i)$ is picked from some arbitrary probability distribution with values in $N$ , and $D (2 i + 1) = D (2 i)$ . Then the mechanism that sums all records might be in NPr, but cannot be in CausDP. Indeed, if $D \sim θ$ , then $\sum_{i} D (i)$ will always be even, but changing one record without modifying its duplicate can make the sum odd.

This last example that finding a special case where NPr implies CausDP is likely difficult. There is, however, a special case where both are equivalent: the absence of dependencies in the data. If changing one record does not influence other records, then NPr and CausDP are equivalent. This result is similar to Corollary 2 in [36], but is simpler and without the change in parameters.

Proposition 22. Let $Θ$ be a family of probability distributions such that for all $θ \in Θ$ and all $ˆ B \in B$ , the random variables ${D (i)}_{| θ, ˆ B}$ are mutually independent. Then a mechanism $M$ is $(Θ, ε)$ -NPr iff it is $(Θ, ε)$ -CausDP.

Proof. Under these conditions, ${D_{- i}}_{| θ, ˆ B, D (i) = t}$ is the same as ${D_{- i}}_{| θ, ˆ B, D (i) = t^{'}}^{'}$ ; as an immediate consequence, $M {(D)}_{| θ, ˆ B, D (i) = t^{'}}^{'}$ is the same as $M {(D_{i \to t^{'}}^{'})}_{| θ, ˆ B, D (i) = t}$ . The statement follows. □

This natural property, combined with the better behavior of CausDP in scenarios like Example 2, might seem like CausDP is a better alternative to CausDP, when one wants to capture an attacker with partial knowledge, under the causal interpretation of differential privacy. However, even with this fix, when records are not independent, CausDP is not always safe to use. We present an example from Adam Smith (personal correspondence, 2018-09-28) showing that a slightly modified version of the identity function can still be CausDP if records are strongly correlated.

Example 5. Let $θ$ output $3 n$ triplicated records: for all $i < n$ , $D_{3 i}$ is picked from some probability distribution $R$ , and $D (3 i + 1) = D (3 i + 2) = D (3 i)$ . Let $M$ be a mechanism that “corrects” a modified record: if there is a record value $x$ appearing only once, and a value $y$ appearing only twice, then $M$ changes the record $x$ to $y$ ; then $M$ always outputs the entire database. It is easy to check that $M$ is $({θ}, 0)$ -CausDP.

This example is more artificial than Example 2, as the mechanism itself “cheats” to use dependencies in the data. Nonetheless, it shows that some mechanisms that leak the full database can be CausDP. Thus, using CausDP as a privacy measure of a given mechanism is dangerous if no information about the mechanism is known. We do not know whether more natural mechanisms could lead to similar counterexamples, for certain classes of probability distributions; but it is clear that simply applying the same technique as the causal variants of [368] is insufficient to solve entirely the problems with correlations under partial knowledge.

Imposing an additional criterion on the definition

In this section, we propose a criterion that the distribution $θ$ must satisfy before NPr can be used. We argue that when this criterion is not satisfied, NPr is not a good measure of the privacy of a mechanism. But when it is satisfied, we obtain natural properties that are false in general: NPr and CausDP are equivalent, and attackers with more partial knowledge are stronger.

We mentioned previously that NPr was not monotonous: an attacker with more knowledge can be considered to be less powerful. In Example 1, an attacker $A$ who did not know $μ$ can learn $μ$ by observing $M (D)$ . This increases their knowledge about $D (i)$ : they now know that $D (i)$ is probably around $μ$ , a fact previously unknown. However, an attacker $B$ , who already knew $μ$ , does not increase their knowledge as much when observing $M (D)$ . Example 2 and Example 5 show that DistDP and CausDP also suffer from this issue. How can we fix this problem? The informal goal is that an attacker with more background knowledge should gain more information. We must make sure that the privacy quantification $ε$ cannot be artificially inflated by non-sensitive information learned by the attacker.

In all previous examples, the attacker’s partial knowledge is strongly correlated with the sensitive information. Thus, $ε$ does not measure the privacy loss due to the mechanism, but also takes into account the prior knowledge from the attacker about the sensitive attribute. Modeling the attacker’s uncertainty is necessary to formalize their partial knowledge, but the only thing that should be captured by $ε$ is the mechanism’s privacy leakage. To ensure this is the case, we argue that the partial knowledge must be independent from the sensitive information, and we propose a formalization that enforces this distinction between sensitive information and partial knowledge.

To this end, we propose an alternative way to model the attacker’s uncertainty, and suggest to normalize the distribution $θ$ to cleanly separate sensitive information and partial knowledge. We show that if such a normalization exists, then an attacker with more partial knowledge is more powerful. Thus, the existence of such a normalization is a desirable property for privacy definitions that model an attacker with partial knowledge, and we argue that it should serve as a criterion that must be satisfied before using such definitions, in order to get meaningful results.

How to formalize the intuition that the sensitive information should be separated from the partial knowledge? The core idea is to express $θ$ as the output of a generative function, with independent random parameters. Each possible value of these parameters corresponds to a possible database.

Definition 53 (Normalization of data-generating distributions). A normalization of a probability distribution $θ$ is a family of mutually independent random variables $(ϕ_{0}, \dots, ϕ_{k})$ , and an injective, deterministic function $ˆ θ$ , such that $θ = ˆ θ (ϕ_{0}, \dots, ϕ_{k})$ .

A normalization de-correlates the distribution: it splits its randomness into independent parts $ϕ_{i}$ . The $ϕ_{i}$ can then play distinct roles: one parameter can capture the sensitive property, while the others can model the attacker’s partial knowledge. We capture this additional requirement in the following definition.

Definition 54 (Acceptable parameters). Given a distribution $θ$ with values in $D \times B$ , an acceptable normalization of $θ$ at index $i$ is a normalization $ˆ θ (ϕ_{0}, \dots, ϕ_{k})$ where:

1.: $ϕ_{0}$ entirely determines the sensitive attribute $D (i)$ : there exists a function $f$ such that for all possible values of $D (i)$ , $P_{θ} [f (ϕ_{0}) = D (i)] = 1$ .
2.: Some of the $ϕ_{1}, \dots, ϕ_{k}$ entirely determine the partial knowledge: there exists $I \subseteq {1, \dots, k}$ and an injective function $g$ such that $P_{θ} [g ({(ϕ_{j})}_{j \in I}) = B] = 1$ .

A family of distributions $Θ$ is acceptable if each $θ \in Θ$ has an acceptable normalization at all indices $i$ .

In practice, we can simply consider a family ${(ϕ_{j})}_{j \in I}$ for some $I$ to be the attacker’s partial knowledge, rather than using a bijection. When partial knowledge is defined using a subset of parameters, an attacker has more partial knowledge when they know more parameters.

Informally, $ϕ_{0}$ must contain enough information to retrieve the sensitive attribute, and the partial knowledge must be independent from it. How can we normalize the $θ$ in Example 1? We cannot have one parameter for $μ$ , and $n$ parameters for the noise added to each record: the sensitive attribute $D (i)$ would require two parameters to express. Rather, $ϕ_{0}$ could be a pair containing both $μ$ and the noise added at $i$ , $D (i) - μ$ . The attacker’s partial knowledge can be $D (j) - μ$ , for $j \Leftrightarrow i$ , without $μ$ . In other words, $μ$ itself is also sensitive. What if we do not want to consider $μ$ as sensitive? Then, $ϕ_{0}$ can be the value of the noise added to the record $i$ , $D (i) - μ$ , and $μ$ is another parameter that can (or not) be part of the attacker’s partial knowledge.

As this example shows, this separation between the partial knowledge and the sensitive value forces us to carefully choose the sensitive value, and it prevents us from comparing scenarios where the sensitive value varies. This formalism can now be used to precisely define the relative strength of two attackers, based on their partial knowledge, and show that an attacker with more knowledge is more powerful.

Definition 55 (Relative strength of partial knowledge). Given probability distributions $θ_{1}$ and $θ_{2}$ with values in $D \times B$ , we say that $θ_{1}$ has more background knowledge than $θ_{2}$ if the three following conditions are satisfied.

1.: $D_{| θ_{1}} = D_{| θ_{2}}$ : the only difference between the probability distributions is the partial knowledge.
2.: For all $i$ , there exists an acceptable normalization $ˆ θ (ϕ_{0}, \dots, ϕ_{k})$ given $i$ that is common to $θ_{1}$ and $θ_{2}$ .
3.: For all $i$ , if we denote $I_{1}$ and $I_{2}$ the set of parameters that correspond to $θ_{1}$ and $θ_{2}$ respectively in this acceptable normalization, then $I_{1} \supseteq I_{2}$ .

Given two families of probability distributions $Θ_{1}$ and $Θ_{2}$ , we say that $Θ_{1}$ has more background knowledge than $Θ_{2}$ if for all $θ_{2} \in Θ_{2}$ , there exists $θ_{1} \in Θ_{1}$ such that $θ_{1}$ has more background knowledge than $θ_{2}$ .

Proposition 23. Let $Θ_{1}$ and $Θ_{2}$ be two families of distributions such that $Θ_{1}$ has more background knowledge than $Θ_{2}$ . If a mechanism $M$ satisfies $(Θ_{1}, ε)$ -NPr, it also satisfies $(Θ_{2}, ε)$ -NPr.

Proof. Suppose that $M$ is $(Θ_{1}, ε)$ -NPr. For a distribution $θ_{2} \in Θ_{2}$ and an index $i$ , let $θ_{1} \in Θ_{1}$ be such that $θ_{1}$ is stronger than $θ_{2}$ . By definition, there exists an acceptable normalization $ˆ θ (ϕ_{0}, \dots, ϕ_{k})$ common to $θ_{1}$ and $θ_{2}$ . Let $f$ be the function extracting the sensitive value from $ϕ_{0}$ in this normalization. Denoting $I_{1}$ and $I_{2}$ the set of parameters corresponding respectively to $θ_{1}$ and $θ_{2}$ , as a simplification, we assume that $I_{2} = \emptyset$ and $I_{1} = {1}$ ; it is straightforward to adapt the proof to the more generic case. For any output $O$ , and all values $t, t^{'} \in T$ , we can decompose:

\begin{matrix} P [M (D) = O | f (ϕ_{0}) = t] = \sum ˆ B P [ϕ_{1} = ˆ B ∣ ∣ f (ϕ_{0}) = t] \cdot P [M (D) = O ∣ ∣ f (ϕ_{0}) = t, ϕ_{1} = ˆ B] . \end{matrix}

The $ϕ_{i}$ are independent: $P [ϕ_{1} = ˆ B ∣ ∣ f (ϕ_{0}) = t]$ is the same as $P [ϕ_{1} = ˆ B ∣ ∣ f (ϕ_{0}) = t^{'}]$ . Since $M$ satisfies $(Θ_{1}, ε)$ -NPr, we also have for all $ˆ B$ :

\begin{matrix} P [M (D) = O ∣ ∣ f (ϕ_{0}) = t, ϕ_{1} = ˆ B] \leq e^{ε} P [M (D) = O ∣ ∣ f (ϕ_{0}) = t^{'}, ϕ_{1} = ˆ B] . \end{matrix}

Thus:

\begin{matrix} P [M (D) = O | f (ϕ_{0}) = t] & \leq e^{ε} \sum ˆ B P [ϕ_{1} = ˆ B ∣ ∣ f (ϕ_{0}) = t^{'}] \cdot P [M (D) = O ∣ ∣ f (ϕ_{0}) = t^{'}, ϕ_{1} = ˆ B] \leq e^{ε} P [M (D) = O ∣ ∣ f (ϕ_{0}) = t^{'}] \end{matrix}

and thus, $M$ satisfies $(Θ_{2}, ε)$ -NPr. Adapting the proof to cases where $I_{1} \subseteq I_{2}$ is straightforward. □

This proposition states that, for acceptable distributions, partial background knowledge can be formalized in a reasonable and intuitive way, guaranteeing that attackers with more background knowledge are stronger. Another advantage is that when this criterion holds, NPr and CausDP are equivalent.

Proposition 24. If $Θ$ is an acceptable distribution, then for any $ε$ and $δ$ , $(Θ, ε, δ)$ -NPr is equivalent to $(Θ, ε, δ)$ -CausDP.

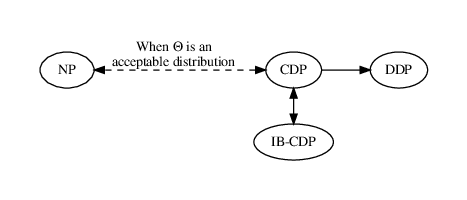
The proof is the same as for Proposition 22. Figure 3.1 summarizes the relations between the definitions introduced in this section.

pict — Figure 3.1: Relations between definitions introduced in Section 3.1.2, assuming $δ = 0$ .

Acceptable normalizations force practitioners to define which information is considered private. If, like in DP, the sensitive information is the value of a given record, with an acceptable normalization, the attacker’s partial knowledge cannot contain records correlated with the target record. This might seem overly restrictive: what if the attacker does know some information correlated with the target record? In this case, one must change the sensitive information to only consider the decorrelated part as sensitive.

To illustrate this process, consider a medical database where the diagnostic records of different patients might be correlated. To find an acceptable normalization, we must choose between two options. The first is to consider attackers that do not have information correlated with the diagnosis of a given patient: in that case, we must protect the information of multiple patients at once, similarly to DP under correlations (a variant of DP defined in [73]). Another option is for the sensitive property to be the diagnosis of someone given the diagnosis of those they are correlated with. We formally present a simpler example below, in Example 6.

Example 6. Consider a referendum, where people vote in pairs, with some amount of correlation between pairs. More precisely, $θ$ is a distribution that generates a database of $2 n$ records according to the following process:

$D (2 i) = 1$ with probability $p_{i}$ , and $0$ with probability $1 - p_{i}$ ;
$D (2 i + 1) = D (2 i)$ with probability $p_{c}$ , and $1 - D (2 i)$ with probability $1 - p_{c}$ .

Suppose the attacker is interested in $D (1)$ . There are two ways of modeling this with an acceptable normalization, depending on whether we want to allow the attacker to know $D (0)$ .

We can pick $ϕ_{i}$ to determine the value of both $D (2 i)$ and $D (2 i + 1)$ . This way, $ϕ_{0}$ is sufficient to know the value of the sensitive information $D (i)$ , and is independent from all $ϕ_{i}$ for $i > 0$ .
We can also pick $ϕ_{2 i}$ to be the event “ $D (2 i) = D (2 i + 1)$ ”, and $ϕ_{2 i + 1}$ to be the value of $D (2 i)$ . In that case, the attacker is allowed to know $D (0)$ , but the sensitive value has changed: the sensitive value is whether $D (0) = D (1)$ ; which is independent from the actual value of $D (0)$ .

LINKPREV LINKUP LINKNEXT